条件概率
条件概率的定义:设$A$, $B$是两个事件,且$P(A)>0$,称
为在事件$A$发生的条件下,事件$B$发生的条件概率。
同理,可得出在事件$B$发生的条件下,事件$A$发生的条件概率为
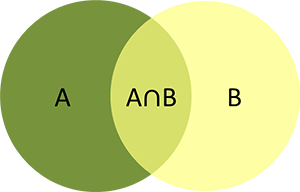
根据文氏图可以看出,在事件$A$发生的情况下,事件$B$发生的概率,就是$P(A \cap B)$除以$P(A)$,即$P(AB)$除以$P(A)$。
乘法定理
设$P(A) > 0$,则有
由条件概率的定义,可得到上述乘法定理。
同理,可得:
$P(AB)$又叫联合概率(两个事件共同发生的概率),还可以记为$P(A \cap B)$或者$P(A,B)$
样本空间及其划分
定义:设$S$为试验$E$的样本空间,$B_1,B_2,\cdots,B_n$为$E$的一组事件。若
(1) $B_i B_j = \emptyset$, $i \neq j$, $ i,j=1,2, \cdots, n$;
(2) $B_1 \cup B_2 \cup \cdots \cup B_n = S$,
则称$B_1 , B_2 , \cdots , B_n $为样本空间$S$的一个划分。
若$B_1 , B_2 , \cdots , B_n $为样本空间$S$的一个划分,那么,对于每次试验,事件$B_1 , B_2 , \cdots , B_n $中必有一个且仅有一个发生。
全概率公式
定理:设试验$E$的样本空间为$S$,$A$为$E$的事件,$B_1 , B_2 , \cdots , B_n$ 为$S$的一个划分,且$P(B_i)>0$ ($i=1,2, \cdots, n$),则
称为全概率公式。
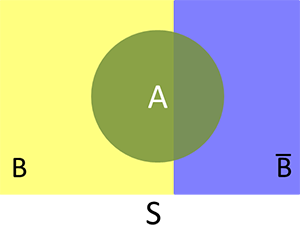
特别地,当$n=2$,并将$B_1$记为$B$,此时$B_2$就是$\overline B$, 全概率公式变为
贝叶斯公式
定理:设试验$E$的样本空间为$S$,$A$为$E$的事件,$B_1 , B_2 , \cdots , B_n$ 为$S$的一个划分,且$P(A)>0$,$P(B_i)>0$ ($i=1,2, \cdots, n$),则
称为贝叶斯公式。
证明:由条件概率的定义及全概率公式即得
特别地,当$n=2$,并将$B_1$记为$B$,此时$B_2$就是$\overline B$, 贝叶斯公式变为
其中,$P(B)$称为$B$的先验概率,即在事件$A$发生之前,我们对$B$事件发生概率的一个基本判断,往往是基于以往的数据分析得到的。$P(B|A)$称为$B$的后验概率,即在$A$事件发生之后,我们对$B$事件发生的概率进行重新评估。
$A$和$B$只是表示事件的符号而已,类似地,贝叶斯公式也可被写为:
此时,$P(A)$称为$A$的先验概率,即在事件$B$发生之前,我们对$A$事件发生概率的一个基本判断,往往是基于以往的数据分析得到的。$P(A|B)$称为$A$的后验概率,即在$B$事件发生之后,我们对$A$事件发生的概率进行重新评估。
举例
例1. 已知人群中某种疾病的发病率为0.001。现有一种试剂可以检验是否患有该疾病,在患病情况下,有99%的可能呈现阳性。没患病情况下,也有5%的可能呈现阳性。现有一个人被检出阳性,请问他确实患有该病的可能性有多大?
解:以$A$表示事件“检验结果呈现阳性”,$B$表示事件“患病”。
已知$P(B)=0.001$,这是先验概率,即没有检查之前,预计的患病可能性,根据人群的历史发病数据得来的。
现在要求$P(B|A)$,就是后验概率,即检查为阳性之后患病的可能性。
参考文献:
[1] 盛骤, 谢式千, 潘承毅. 概率论与数理统计(第四版)[M]. 北京: 高等教育出版社, 2008.
